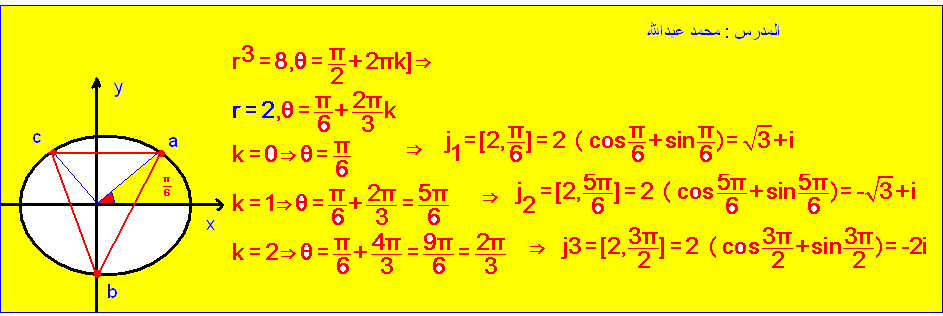مجموعة الأعداد المركبة (
العقدية)K
|
مفردات |
النشاطات والأساليب والوسائل |
|
1.
العدد العقدي( المركب)
2.
جمع الأعداد المركبة
وطرحها
3.
ضرب الأعداد المركبة وقسمتها
4.
الشكل المثلثي للعدد المركب
5.
الجذور التربيعية للعدد المركب
6.
حل معادلات الدرجة الثانية في مجموعة الأعداد المركبة
7.
الجذور التكعيبية للواحد
|
1.
توضيح أن معادلة بسيطة مثل
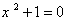 ليس
لها حل في مجموعة الأعداد الحقيقية يستدعي وجود مجموعة جديدة من
الأعداد يكون فيها حلول لمثل هذه المعادلة . ليس
لها حل في مجموعة الأعداد الحقيقية يستدعي وجود مجموعة جديدة من
الأعداد يكون فيها حلول لمثل هذه المعادلة .
2.
يتم تعريف العدد المركب بأنه عدد على الصورة  ((y,x
عددان حقيقيان ، كما يتم استنتاج أن مجموعة الأعداد الحقيقية هي مجموعة
جزئية من مجموعة الأعداد المركبة ، وتعطى أمثلة
وتدريبات على الأعداد المركبة وعلى إيجاد قوى العدد (i)
. ((y,x
عددان حقيقيان ، كما يتم استنتاج أن مجموعة الأعداد الحقيقية هي مجموعة
جزئية من مجموعة الأعداد المركبة ، وتعطى أمثلة
وتدريبات على الأعداد المركبة وعلى إيجاد قوى العدد (i)
.
3.
تقديم عمليات الجمع والطرح والضرب على الأعداد المركبة
وتدريبات عليها، أما القسمة فيقدم قبلها مفهوما المرافق والمقياس للعدد
المركب ثم تقدم تدريبات عليها .
4.
قبل تقديم الجذور التربيعية يوضح معنى تساوي عددين
مركبين ، ثم نستخدم تعريف الجذر التربيعي ثم تكون المعادلات المناسبة
لإيجاد الجذور التربيعية المطلوبة .
5.
في حل معادلات الدرجة الثانية تعالج المعادلات ذات
المعاملات الحقيقية التي مميزها سالب فيكون جذراها مترافقين ، كما
يعالج موضوع تكوين معادلة إذا علم جذراها .
6.
يتم إيجاد الجذور التكعيبية الثلاثة للواحد بحل
المعادلة
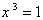 في
مجموعة الأعداد المركبة ثم إيجاد جذور تكعيبية لأعداد حقيقية أخرى
باستخدام الجذور التكعيبية للوحدة . في
مجموعة الأعداد المركبة ثم إيجاد جذور تكعيبية لأعداد حقيقية أخرى
باستخدام الجذور التكعيبية للوحدة .
7.
الإشارة عند الحاجة وفي موضعها إلى دور العلماء
المسلمين في الأعداد المركبة
.
|
تمهيد :
لما كانت بعض المعادلات من الشكل
x+a=b مستحيلة الحل في البنية (+,N)
كالمعادلة 3 =7+x
أحدث الباحثون مجموعة الأعداد الصحيحة Q :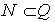
بإحداث الأعداد السالبة فأصبح حل هذه المعادلة
ممكناً في البنية (+,Q) وحله
4 =(7-)+
3= x ولما كانت بعض المعادلات من الشكل
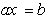 مستحيلة الحل
في
مستحيلة الحل
في
(*,Q)
كالمعادلة 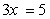 أحدث الباحثون مجموعة الأعداد
العادية وحل هذه المعادلة
أحدث الباحثون مجموعة الأعداد
العادية وحل هذه المعادلة 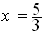 ولما كانت بعض المعادلات من الشكل
ولما كانت بعض المعادلات من الشكل 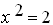 مستحلة في
الاعداد العادية
مستحلة في
الاعداد العادية
أحدث الباحثون مجموعة الأعداد الحقيقية
R ومع ذلك بقي ان المعادلة
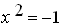 بدون حل لذلك قام الباحثون ما سمي بالوحدة
التخيلية عن عدد مربعه يساوي (1-) رمزه
i
بدون حل لذلك قام الباحثون ما سمي بالوحدة
التخيلية عن عدد مربعه يساوي (1-) رمزه
i
تعريف و تسميات :
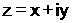
z
عدد عقدي مؤلف من جزئين الأول الصحيح
x
والثاني التخيلي
y والعدد
i يدل على القسم
التخيلي
ملاحظات : العمليات
الأربعة على الأعداد العقدية
- الجمع والطرح : مثل جمع أي ثنائيتن ( القسم الحقيقي مع
القسم الحقيقي و القسم التخيلي مع القسم التخيلي
وكذلك بالنسبة للطرح
- التقسيم : نضرب البسط والمقام بمرافق
المقام
المرافق : ليكن العدد العقد
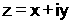 مرافقه هو
مرافقه هو
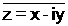 علماً ان المرافق فقط تغير اشارة القسم
التخيلي
علماً ان المرافق فقط تغير اشارة القسم
التخيلي
القوى الطبيعية للعنصر
التخيلي i :
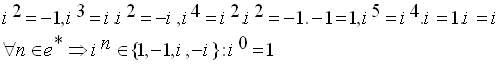
مثال:
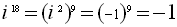
خواص المرافق :
أولاً: ليكن لدينا العدد
العقدي 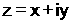
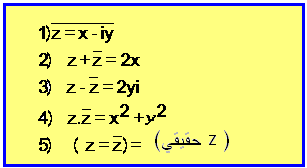
ثانياً : ليكن
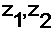 عددين مركبين ( عقديين )
عددين مركبين ( عقديين )
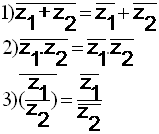
حل المعادلات في
K :
أولاً :
المعادلة من الشكل 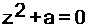 :
:
1) إذا كان
a سالباً مثال
:
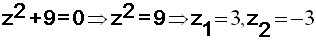 للمعادلة
جذران حقيقيان
للمعادلة
جذران حقيقيان
2) إذا كان
a موجباً مثال :
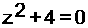
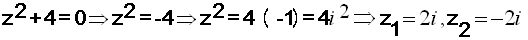 للمعادلة
جذران تخيليان
للمعادلة
جذران تخيليان
ًثانياً :
المعادلة من الشكل :
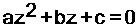
مميز هذه المعادلة :
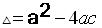
1) عندما
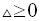 للمعادلة جذران حقيقيان هما كما تعلم
للمعادلة جذران حقيقيان هما كما تعلم
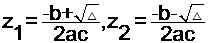
2) عندما
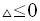 للمعادلة جذران تخيليان هما
للمعادلة جذران تخيليان هما
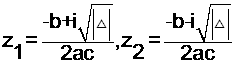
مثال : حل المعادلة :
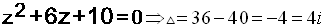
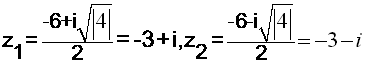
القيمة المطلقة للعدد المركب
:
تعريف : القيمة
المطلقة للعدد المركب z (ونرمز لها
 ) هي بالتعريف الجذر التربيعي الموجب لحاصل
ضرب z بمرافقه أي أن
) هي بالتعريف الجذر التربيعي الموجب لحاصل
ضرب z بمرافقه أي أن
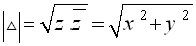
حالة خاصة :
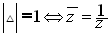 برهان :
برهان :
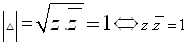
تمثيل العدد المركب في مستو محدث
بمعلم متجانس :
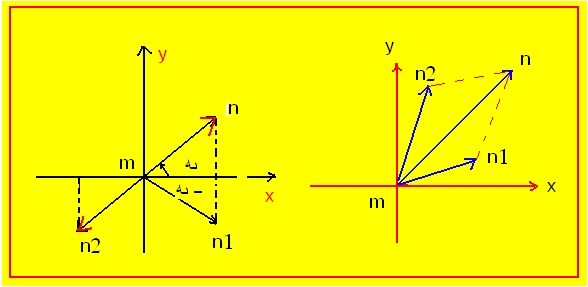
في مستو محدث بمعلم متجانس يمكننا أن نقابل كل عدد
مركب 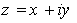 بشعاع طلق ممثله الشعاع المقيد
بشعاع طلق ممثله الشعاع المقيد
x,y)n )صورة
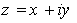
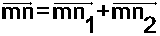 صورة
صورة 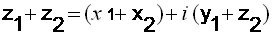
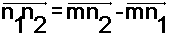 صورة
صورة
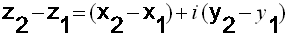
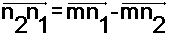 صورة
صورة
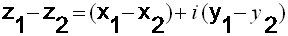
الشكل المثلثي للعدد المركب
( غير معدوم ):
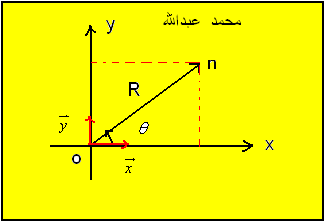
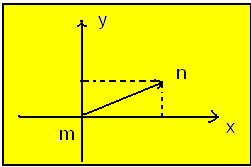
ليكن العدد المركب
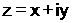 كما هو موضح بالشكل نسمي
كما هو موضح بالشكل نسمي
 عمدة العدد المركب
z :
عمدة العدد المركب
z :
يمكن حساب R
من العلاقة التالية 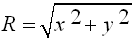 وكذلك
وكذلك 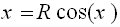 و
و
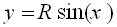
وبالتعويض في العدد العقدي ( المركب
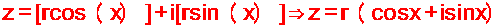
وهو الشكل المثلثي للعدد العقدي والشكل
المختصر للعدد العقدي 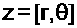
نتائج من تعريف الشكل المثلثي
للعدد المركب :

جداء
عددين عقدين بالشكل المثلثي:
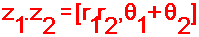
رفع عدد مركب بشكله المثلثي الى
أس طبيعي : 
حالة خاصة :
قسمة عدد مركب على آ خر بالشكل
المثلثي:

الجذور من المرتبة
n لعدد عقدي بالشكل المثلثي
n ينتمي الى {1 - 2 - 3 - 4 }:
مثال :
أوجد الجذور التكعيبية للعدد المركب
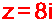 وعين صور هذه
الجذور في المستوي المحدث
وعين صور هذه
الجذور في المستوي المحدث
الحل :
نكتب z بالشكل المثلثي فنجد
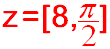 ونفرض
ونفرض
 جذرا تكعبياً للعدد z
جذرا تكعبياً للعدد z
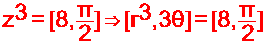 وحسب
تساوي عددين عقديين بالشكل المثلثي نجد :
وحسب
تساوي عددين عقديين بالشكل المثلثي نجد : 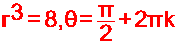
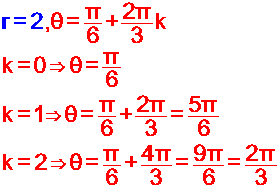 فالعدد
العقدي
فالعدد
العقدي 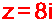 له في k
ثلاثة جذور تكعيبية هي
له في k
ثلاثة جذور تكعيبية هي
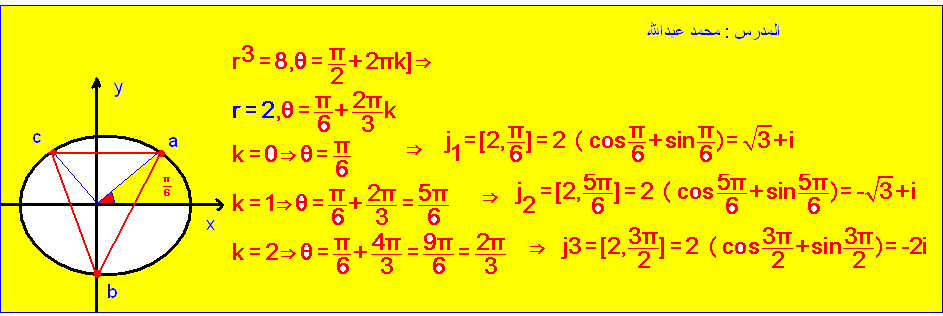
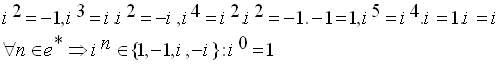
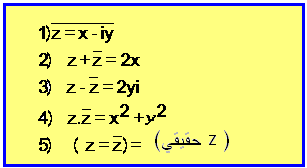
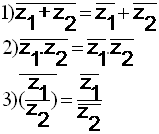
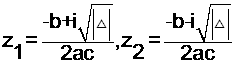
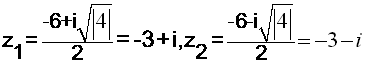



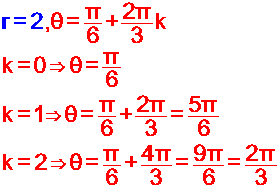 فالعدد
العقدي
فالعدد
العقدي