المحددات - المعادلات الخطية

المحددات

المحددات من المرتبة الثانية: رمز المحدد ∆

إذا كانت    أعداد حقيقية فإن العدد الحقيقي  نكتبه بالشكل  ونسميه محدداَ من المرتبة الثانية ونسمي

    قيمة المحدد    

مكونات المحدد :  a, b     السطر الاول      السطر الثاني       العمود الاول          العمود الثالث

المحددات من المرتبة الثالثة :

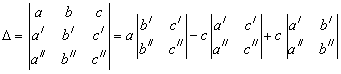
وبالتالي المحددات من المرتبة الثانية واضحة في الأعلى

بعض خواص المحدد:( وتشمل هذه الخواص المحدد من جميع المراتب )

 1- لا تتغير قيمة المحدد إذا استبد لنا أسطره بأعمدته بالترتيب ذاته

2- لا تتغير قيمة المحدد إذا نشر وفق عناصر أي سطر منه (أو أي عمود) مع مراعات تناوب الإشارات وأخذ بالإشارة الموجبة

3- لا تتغير قيمة المحدد إذا ضربنا أحد أسطره( أو أعمدته) بعدد حقيقي وجمعنا النتائج بالترتيب مع عناصر سطر آخر (أو عمودٍ آخر)

4- إذا ضربنا عناصر أحد الأسطر (  أو أحد الأعمدة) بعدد حقيقي فإن قيمة المحدد الناتج تساوي ناتج ضرب قيمة المحدد بالعدد الحقيقي

المعادلات الخطية

تعريف المعادلة الخطية : هي المعادلة التي تكون حدودها ( الحاوية للمجاهيل )حدوداَ من الدرجة الأولى بالنسبة إلى تلك المجاهيل

حل المعادلة الخطية يعني إيجاد قيم المجاهيل التي تحقق المعادلة المعطى

المعادلة ذات مجهول واحد :

الشكل العام لهذه المعادلة   a x = b

مناقشة الحل :  1) إذا كان  للمعادلة حل وحيد 

                 2) إذا كان  a = 0 نميز حالتين :

                                *)   a = 0, b≠0  المعادلة مستحيلة

                                *)    a = 0    b = 0  للمعادلة عدد غير منته من الحلول , مجموعة حلولها هي  R

المعادلة :    (0≠ ax + by = c     ( a . b  :

  مناقشة الحل

         1) تقبل عدداَ غير منته من الحلول .

         2) من أجل كل قيمة لأحد المجهولين نجد قيمة للمجهول الآخر

        3) كل معادلة خطية بأكثر من مجهول وأمثال كل مجهول لا يساوي الصفر لها عدد غير منته من الحلول

الحل المشترك لمجموعة معادلتين خطيتين بمجهولين:

الشكل العام   

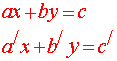
مناقشة الحل :

أولاَ) إذا كان   0 ≠∆   لمجموعة المعادلتين حل مشترك وحيد        

ثانياَ)   إذا كان 0=∆    نميز حالتين :

         الحالة الأولى :  0=∆      و   ( ) أو ( )

                        ليس لمجموعة المعادلتين حل   مشترك (  المجموعة مستحيلة الحل )

          الحالة الثانية :  0=∆  و(    و  )

للمجموعة عدد غير منته من الحلول وهي حلول إحدى المعادلتين لأن إحداهما ناتجة عن الأخرى بضربها  بعدد حقيقي غير معدوم

         حالة خاصة :  إذا كان0 =( c, ) فإن مجموعة المعادلتين

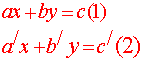
نسمي كلاَ من معادلتي المجموعة معادلة خطية متجانسة ( هي مجموعة خطية متجانسة )

مناقشة الحل :

              1)     حل مشترك لهذه المجموعة نسميه الحل الصفري

              2)  0 ≠∆  يكون الحل الصفري وحيداَ  

              3)   0  =∆ يكون للمجموعة عدد غير منته من الحلول ( هي حلول إحدى معادلتي المجموعة )

الحل المشترك لمجموعة ذات ثلاث معادلات خطية بمجهولين

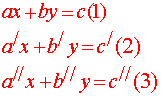
للبحث عن الحل المشترك للمجموعة {(3),(2), (1)  }  نبحث عن الحل المشترك لمجموعة مؤلفة من اثنين من هذه المعادلات كالمجموعة

(1),(2) مثلاً

1) إذا كانت {(1) , (2)} مستحيلة فإن {(3),(2), (1)  } مستحيلة

2) إذا كانت  {(1) , (2)} تقبل حلاً وحيداً نعوض هذا الحل في (3)

                                                *) إذا تحققت (3) يكون للمجموعة  {(3),(2), (1)  } حل مشترك وحيد

                                                 *) إذا لم تحقق (3) تكون المجموعة  {(3),(2), (1)  }مستحيلة الحل

3) إذا كانت  {(1) , (2)} تقبل عدداً غير منته من الحلول فإن المجموعة {(1) , (2)} تكافئ إحدى المعادلتين (1) , (2) عندئذً يؤول حل المجموعة {(3),(2), (1)  } إلى حل المجموعة المكافئة {(2) , (3)} أو {(1) , (3)}

الحل المشترك لمجموعة ذات معادلتين خطيتين بثلاثة مجاهيل

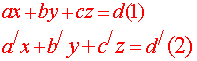
نفرض أحد المجاهيل وليكن z   ثابت ويصبح مناقشة معادلتين بمجهولين

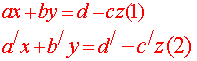
مناقشة الحل :

1)  0 ≠∆ لمجموعة المعادلتين حل وحيد من أجل كل z من  R  فلها عدد غير منته من الحلول

2)  0  =∆    و  (  ) للجملة عدد غير منتهي من الحلول

                لكن (  أو    أو  ) فالمجموعة مستحيلة

نتيجة : إذا كان ( عدد المعادلات أقل من عدد المجاهيل ) في مجموعة تتألف من أكثر من معادلة

        1ً ) إما أن يكون للمجموعة عدد ٌ غير منته من الحلول وإما أنها مستحيلة .

        2ً ) إذا كانت هذه المعادلات متجانسة ( ولأنها تقبل الحل الصفي ) فلها عددٌ غير منته من الحلول

الحل المشترك لمجموعة مؤلفة من ثلاث معادلات خطية بثلاثة مجاهيل

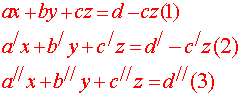
للبحث عن حلول هذه المجموعة نبحث عن حلول مجموعة مؤلفة من أثنتين من معادلات المجموعة المفروضة مثل {(1) , (2)}

1ً) إذا كانت المجموعة {(1) , (2)}  مستحيلة فإن المجموعة {(3),(2), (1)  } تكون مستحيلة .

2ً) إذا كان للمجموعة {(1) , (2)} عدد غير منتهي من الحلول فإن هذه الحلول هي من الشكل    

   ( قد يكون f  أو  h  ثابتاً)  نعوض في (3 ) فنجد معادلة من الشكل   a x = b  وقد سبقت مناقشتها

توظيف المحدد من المرتبة الثالثة للبحث عن حلول مجموعة ذات ثلاث معادلات خطية

أولاً : عندما 0 ≠∆  لمجموعة المعادلات حل وحيد

ثانياً: 0  =∆  و ( أو  أو ) المجموعة مستحيلة

ثالثاً :    0  =∆  و (   )

       مناقشة : نختار مجموعة من معادلتين منها  فإذا لم تكن مستحيلة ولا تنتج إحدى معادلتيها عن الأخرى عندئذً نعد أحد المجاهيل

 ( z مثلاً ) معلوماً ونحسب المجهولين   x , y   بدلالته فنحصل على

نعوض في المعادلة الثالثة فنجد المعادلة   وهذه المعادلة سبقت مناقشتها إذ لها عدد غير منته من الحلول أو إنها مستحيلة فالمجموعة المفروضة لها عدد غير منته من الحلول أو أنها مستحيلة