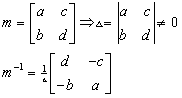مصفوفة تابع خطي
مفردات |
النشاطات والأساليب والوسائل |
|
1. المصفوفة
2. جمع المصفوفات وطرحها
3. ضرب المصفوفات
4. المحددات
5. المقلوب الضربي لمصفوفة
6. حل أنظمة معادلات خطية باستخدام المحددات
7. التفسير الهندسي لحل النظام الخطي . |
1. تقديم المصفوفة باستخدام مثال أو أكثر كوسيلة لتنظيم معلومات عددية في جدول مستطيل الشكل مكون من صفوف وأعمدة . 2. توضيح تساوى مصفوفتين وإعطاء تدريبات على إيجاد عناصر مجهولة في مصفوفتين متساويتين 3. توضيح كيفية إجراء عمليات جمع المصفوفات وطرحها وضرب مصفوفة بعدد بدون استخدام الرموز المجردة . 4. التدرج في تقديم ضرب المصفوفات حيث يمكن البدء بضرب مصفوفة من صف واحد بأخرى من عمود واحد ، ثم مصفوفة من صفين بأخرى من عمود وهكذا … و استنتاج أن ضرب المصفوفات غير تبديلي ثم التعرف على مصفوفة الواحدية كمصفوفة محايدة في عملية ضرب المصفوفات المربعة . 5. تقديم المحددة من الدرجة الثانية المرتبطة بالمصفوفة المربعة من النوع 2×2 وتوضيح أن المحدد تؤول إلى عدد حقيقي ، مع استنتاج بعض خواص المحددات ، ثم تقديم المحددة من الدرجة الثالثة وطريقة حسابها . 6. إيجاد المقلوب الضربي لمصفوفة يقتصر على المصفوفات المربعة من النوع 2×2 . 7. عرض تطبيقات رياضية للمصفوفات من حيث استخدامها لتمثيل بيانات وصفية بصورة مختصرة منظمة ، ومن حيث استخدامها لحل أنظمة معادلات من الدرجة الأولى في مجهولين 8. توضيح كيفية استخدام المحددات من الدرجتين الثانية والثالثة لحل أنظمة معادلات خطية بمتغيرين أو ثلاثة متغيرات مع إعطاء تدريبات كافية على ذلك . 9. يمكن تقديم تمارين إثرائية باستخدام الحاسب الآلي لإجراء بعض التطبيقات على المصفوفات مثل إيجاد محددة ومعكوس مصفوفة مربعة 3×3 ، 4×4 ، … إلخ ، و أي تطبيقات أخرى . 10. تمثيل مجـموعة الحل لنظام من المعادلات الخطية في متغيرين في المستوي الإحداثي .
|
تعريف :
ليكن
![]() تابعاَ خطياَ ولتكن
تابعاَ خطياَ ولتكن
![]() اساساَ في
اساساَ في ![]()
![]()
( فهو عبارة خطية في عناصر الأساس R)ويؤدي
![]() (بشكل وحيد)
(بشكل وحيد)
![]()
فهو عبارة خطية في عناصر الأساس ٌ
![]() (بشكل وحيد)
(بشكل وحيد)
نعرف الكائن الرياضي
![]() بأنه مصفوفة التابع الخطي ب بالنسبة إلى
الأساس G ونرمزها
بأنه مصفوفة التابع الخطي ب بالنسبة إلى
الأساس G ونرمزها ![]() وعند عدم وجود التباس نرمزها بـ m
وعند عدم وجود التباس نرمزها بـ m
ملاحظات تتعلق بالتعريف:
*
a,b العامود الاول
* d , c العامود الثاني
*a , c السطر الأول *
b , d الطر الثاني والمحدد
![]()
مبرهنة:مصفوفة التابع الصفري
![]() هي
هي ![]() وذلك
بالنسبة إلى أي أساس(
وذلك
بالنسبة إلى أي أساس(![]() ,
,![]() )
في
)
في ![]()
تساوي مصفوفتين : نقول عن المصفوفتين التاليتين انهما متساويتين إذا الشرط التالي
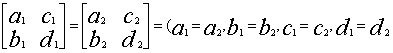
العمليات على المصفوفات :
1- جمع
مصفوفتين: إذا كانت
![]() مصفوفة
مصفوفة
![]() بالنسبة إلى
أساس مفروض R.
بالنسبة إلى
أساس مفروض R.
وكانت ![]() مصفوفة
مصفوفة
![]() بالنسبة إلى
أساس ذاته R.
بالنسبة إلى
أساس ذاته R.
فإن
![]() +
+![]() هي بالتعريف
هي بالتعريف
![]()
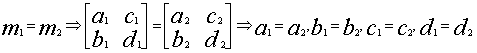
خواص عملية الجمع :
- إن جمع المصفوفات عملية تبديلية
![]()
- إن جمع المصفوفات عملية تجميعية
![]()
- المصفوفة الصفرية هي العنصر الحادي بالنسبة لعملية جمع المصفوفات
-
![]()
-![]()
ضرب المصفوفات :
ضرب مصفوفة بعدد حقيقي :
![]()
ضرب مصفوفتين :
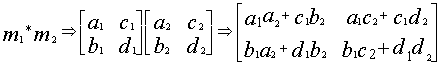
ملاحظة ضرب مصفوفتين ليست تبديلية
خواص عملية الضرب :
1- ضرب المصفوفات عملية تجمعية
![]()
2- العنصر الحيادي بالنسبة لضرب المصفوفات
![]()
مقلوب المصفوفة:
يكون للمصفوفة مقلوب إذا كانت
![]()