دراسة تغيرات تابع عددي
اطراد تابع عددي :
تعريف : ليكن f  تابعاً معرّفاً على وليكن مجالاً محتوى في X     :   
1) نقول إن f متزايد تماماً على إذا وفقط إذا
2) نقول إن f متناقص تماماً على إذا وفقط إذا
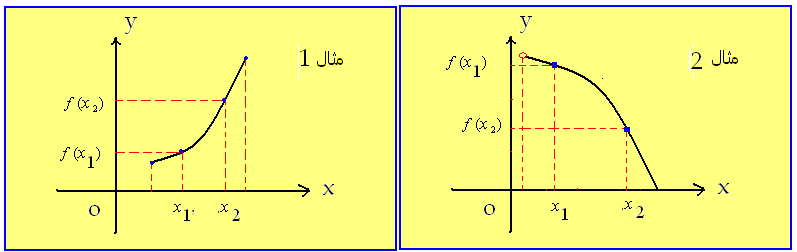
مثال : ليكن f  التابع المعرف على [1,3]  وفق   فإن f متزايد على المجال [1,3] كما في الشكل

مثال 2 : ليكن f  التابع المعرف على [1,3[  وفق:    فإن f  التابع متناقص على [1,3[ كما هو في الشكل السابق
مبرهنة (تقبل بدون برهان): إذا كان f اشتقاقياً على المجال [a,b]  عندئذ:
1) الشرط اللازم والكافي ليكون f متزايد تماماً على ]a,b[  هو أن يكون مشتق f  موجباً على ]a,b[ ولا ينعدم على أي مجال جزئي من هذا المجال.
2)الشرط اللازم والكافي ليكون f متناقص تماماً على ]a,b[  هو أن يكون مشتق f سالباً على ]a,b[ ولا ينعدم على أي مجال جزئي من هذا المجال.
3)الشرط اللازم والكافي ليكون f ثابتاً على ]a,b[  هو أن يكون مشتق f  معدوماًعلى ]a,b[ .
مثال1): f معرف على R وفق :
الدراسة : f  اشتقاقي على R و   إذن ولا ينعدم إلا عند x=1
( أي إن   لاينعدم على أي مجال جزئي من R ) فالتابع f  متزايد تماماً على R .
دراسة تغيرات تابع عددي:
لدراسة تغيرات تابع عددي :  1) نعيّن مجموعة تعريفه على هيئة مجال أو اجتماع مجالات ونعيّن مجالات استمراره
                                   2) نعيّن قيم التابع عند أطراف المجالات المغلقة لمجموعة استمراره ونهايات التابع عند أطراف المجالات المفتوحة
                                   3) ندرس اطراد التابع وفق إشارة مشتقه ( وهذا يتطلب تعيين مجموعة تعريف المشتق) 
ملاحظة : قد ننظم جدولاً بالمعلومات السابقة نسميه( جدول التغيرات)
تمرين : ليكن f  التابع المعرف بالقاعدة   ادرس تغيرات هذا التابع
الحل : التابع صحيح فهو معرّف على R  ومستمر عليها ويقبل عليها الاشتقاق 
    ينعدم المشتق عند  x=0  (جذر مضاعف ) فلا يغير عندها إشارته    و عند x = 3  (جذر بسيط) يغير عندها إشارته  الجدول

 
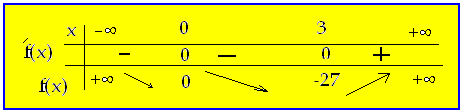
 يدل جدول تغيرات f  متناقص على المجال  ومتزايد تماماً على المجال
مبرهنة (تقبل دون ذكر البرهان ):

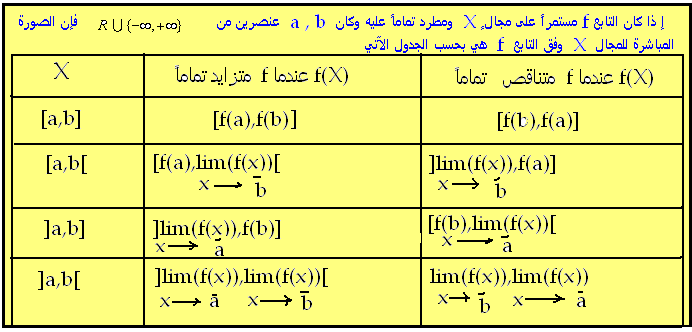
ملاحظة (1) : واضح أنه إذا كان f  ثابتاًعلى مجموعة X  وكانت قيمته الثابته c  فإنأية مجموعة جزئية غير خالية من X  وفق  f  هي {c}
ملاحظة (2) : إذا طلب معرفة صورة مجال من مجموعة تعريف تابع  f  غير مطرد تماماً عليه نجزئ ذلك المجال إلى اجتماع مجالات يكون التابع مطرداً تماماً أو ثابتاً على كل منها ثم نطبق المبرهنة السابقة على كل من هذه المجالات مع ملاحظة أن    

التابع المحدود والتابع غير المحدود :
تعريف : ليكن التابع  f  معرفاً على  :وفق التابع(f(x    
             1) نقول إن التابع محدود من الأعلى إذا وفقط إذا وجد عدد حقيقي L  بحيث 
             2) نقول إن التابع محدود من الأدنى إذا وفقط إذا وجد عدد حقيقي h  بحيث 
            3)   نقول إن التابع محدود  إذا وفقط إذا كان محدوداً من الأعلى ومن الأدنى
ملاحظة : يمكن معرفة محدودية التابع من مجموعة التعريف
مبرهنة :( تقبل بدون برهان ) 
       1)  كل تابع متزايد وغير محدود من الأعلى يسعى إلى
      2) كل تابع متناقص وغير محدود من الأدنى يسعى إلى
     3) كل تابع مستمر على مجال محدود مغلق هو تابع محدود
القيم الكبرى والقيم الصغرى محلياً :
تعريف : ليكن f  التابع المعرف على   وليكن
 1) نقول إن    قيمة كبرى محلياً للتابع  f إذا وفقط إذا وجد مجال مفتوح  يضم   بحيث 
 2)   نقول إن    قيمة كبرى محلياً للتابع  f إذا وفقط إذا وجد مجال مفتوح  يضم   بحيث 
مبرهنة (بدون برهان ): ليكن التابع f مستمراً على المجال ]a,b[   واشتقاقياً على كل من المجالين     عندئذً
 1) إذا كان   على المجال  وكان    على المجال  كان     قيمة كبرى محلياً للتابع f .
 2) إذا كان     على المجال   وكان   على المجال       كان        قيمة صغرى محلياً للتابع f .
ملاحظة هامة : يوجد في بعض الحالات مشتق التابع f  غير معرف وغير قابل للأشتقاق عند   و قيمة صغرى أو كبرى محلية
ملاحظات :    1) إذا كان  وكان  قيمة كبرى(أو صغرى ) محلياً للتابع f وكان f اشتقاقيا عند  كان
                2) إن قيمة كبرى محلياً ليست بالضرورة أكبر قيم التابع كما أن قيمة صغرى محلياً ليست بالضرورة أصغر قيم التابع .
                3) إذا كان أكبر قيم التابع f المعرف على   كان قيمة كبرى محلياً عندئذ   وبالمثل
                      إذا كان أصغر قيم التابع f المعرف على   كان قيمة صغرى محلياً عندئذ
                    4) قد يكون لتابع f أكثر من قيمة كبرى محلياً وقد يكون له أكثر من قيمة صغرى محلياً
                5) إذا كان التابع  f  مطرداً تماماً على مجال مفتوح فليس له في هذا المجال قيم كبرى ( ولا قيم صغرى) محلياً .
                6) إذا كان التابع f  ثابتاً على المجال عندئذ قيمة الثابتة هي قيمة كبرى محلياً له وهي قيمة صغرى محلياً له عند كل .
توظيفات لدراسة تغيرات تابع عددي:
البحث عن جذور معادلة أوحلول متراجحة
نظرية القيمة الوسطى : إذا كانت f  مستمرا على المجال [a,b]  عندئذ أياً كان العدد الحقيقي h  المحصور بين  و وجد على الأقل عدد حقيقي
                           
                           أي إن للمعادلة    ( بالمجهول x )والمكافئة   جذراً واحداً على الأقل في المجال [a,b]
حالة خاصة :إذا كان f  مستمراً على المجال [a,b]  ومطرداً تماماً على هذا المجال وكان h  محصوراً بين   و   عندئذً للمعادلة
بالمجهول x حل وحيد في المجال [a,b]

جهة التقعر

اصطلاح:  نقول إن النقطة  تقع فوق النقطة إذا كان   وكذلك  نقول إن النقطة  تقع تحت النقطة إذا كان
تعريف : ليكن الخط البياني للتابع f  الاشتقاقي على المجال المفتوح X
   أولاً : نقول إن الخط البياني يتقعر على المجال ْ نحو العينات الموجبة إذا وفقط إذا كانت جميع نقاط الخط البياني واقعة فوق المماس له في هذا المجال ما عدا نقطة
       التماس .
   ثانياً : نقول إن الخط البياني يتقعر على المجال ْ نحو العينات السالبة إذا وفقط إذا كانت جميع نقاط الخط البياني واقعة تحت المماس له في هذا المجال ما عدا نقطة        التماس .
     أو       التقعر نحو العينات الموجبة      و     التقعر نحو العينات السالبة
المستقيمات المقاربة
أولاً :  إذا كان      ( ثابت ) فإن         مستقيم مقارب وهذا يكافئ   

ثانياً :   بدراسة إشارة الفرق :   فإن        1ً)    فإ ن الخط البياني فوق مستقيم  
                                                                2ً)  فإن الخط البياني تحت المستقيم
ثالثاً : إذا كان عندئذ   x=a  مقارب يوازي محور العينات

رابعاً : إذا كان   فإن مستقيم مقارب مائل