| الصفحة الرئيسية | مقدمة | الأهداف | الرياضيات 1 | الرياضيات2 | رياضيات3 | المنتدى | المصادر | البحث | عداد الزوار | من نحن | اتصل معنا |
التابع الأصلي :
تعريف :
ليكن ب تابعاً عددياً معرفاً على المجال ![]() نقول إن التابع F تابع أصلي
على المجال X إذا كان وفقط إذا كان F
اشتقاقياً على X
ويحقق
نقول إن التابع F تابع أصلي
على المجال X إذا كان وفقط إذا كان F
اشتقاقياً على X
ويحقق
![]() الأمثلة
: ليكن لدينا التوابع الأصلية التالية اوجد تابع لكل منها
الأمثلة
: ليكن لدينا التوابع الأصلية التالية اوجد تابع لكل منها
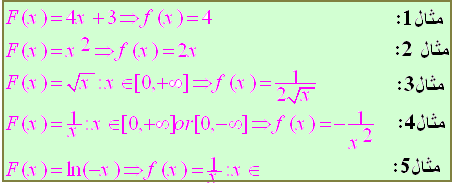
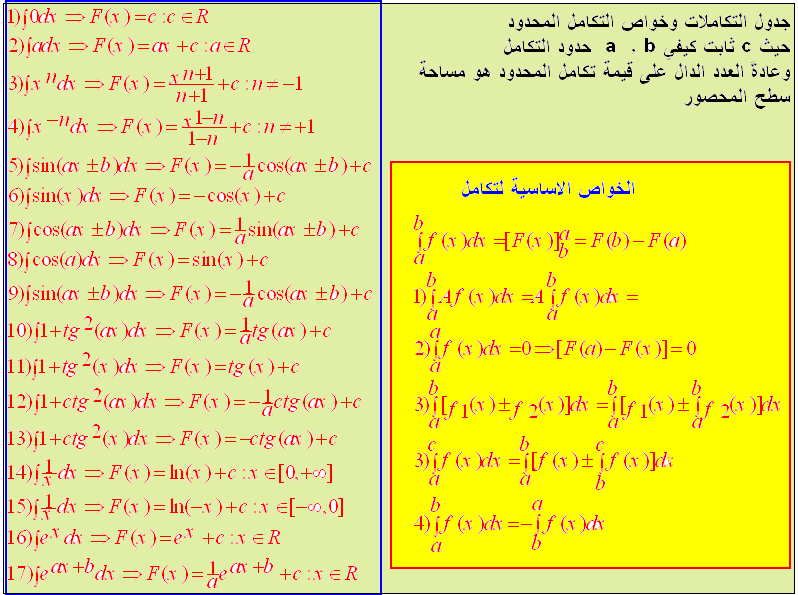
الأمثلة محلولة:اوجد قيمة التكاملات التالية:
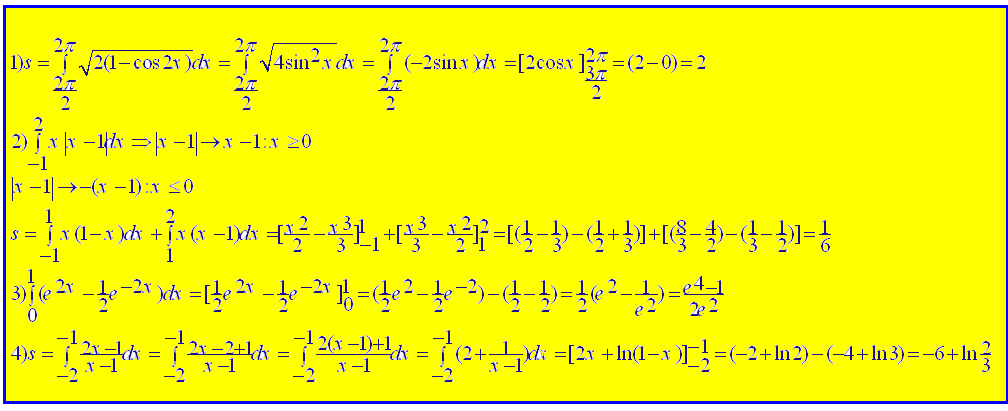
تمارين الفصل الخامس:
في التمارين من الرقم من 1 حتى 11 أوجد مجموعة التوابع الأصلية للتابع f على المجال X .
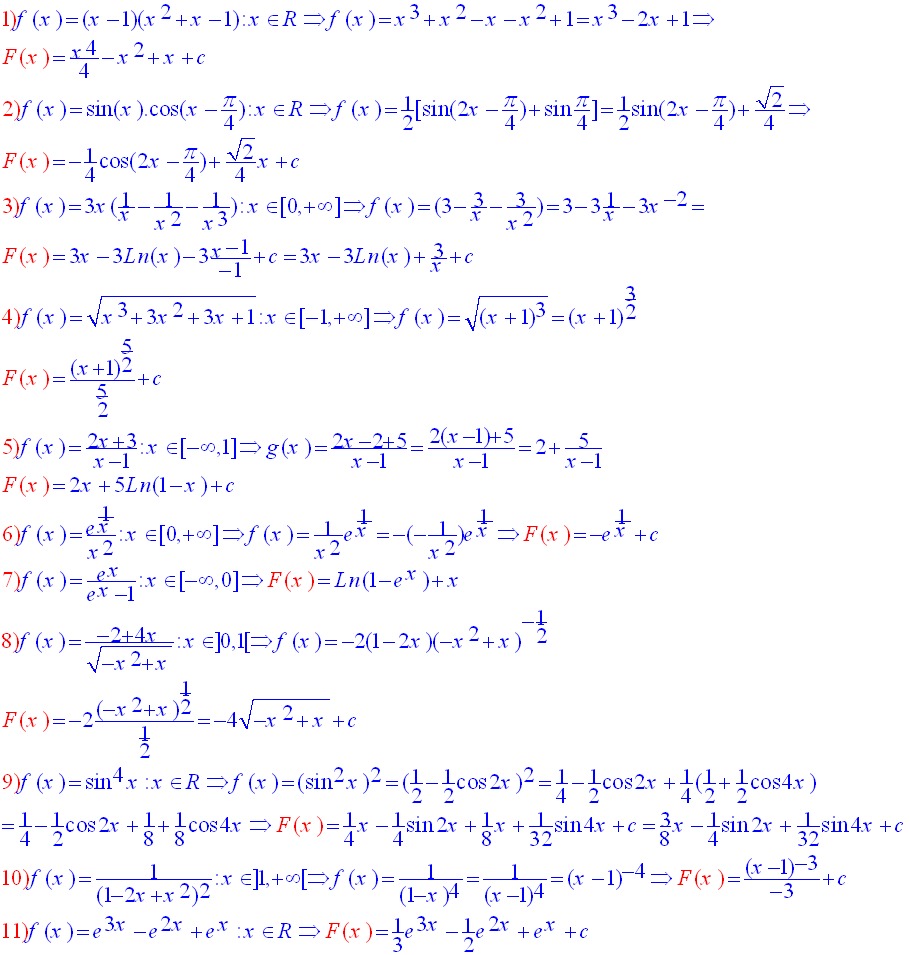
في التمارين من 12 حتى 17 اوجد قيمة التكاملات التالية:
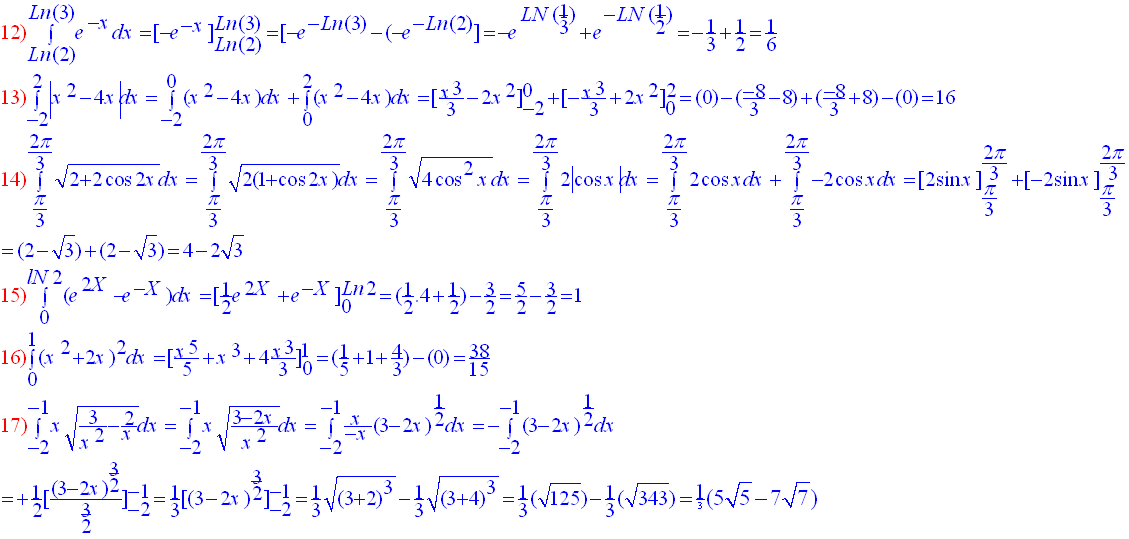
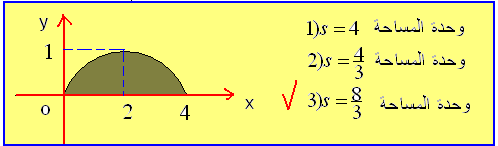
18) في الشكل المجاور s هي مساحة السطح المظلل المحصور بين خط البياني لنابع f والمحور ox ثلاث قيم مقترحة لهذهالمساحة واحدة منها فقط صحيحة دل على القيمة الصحيحة
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
19) ليكن ؟ الخط البياني
للتابع
f المعرف على
{1 } \ R
وفق : ![]()
1) احسب مساحة السطح المحصور بين
الخط البياني والمحور السينات ox والمستقيمين
x=2 ![]()
2) احسب مساحة السطح المحصور بين ؟ الخط البياني ox والمستقيمين x=-3 x=-2
الحل : نرسم ؟ الخط البياني
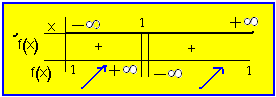
نقاط مساعدة (0 ,2)n 2 (0 ,2) n2
الحل :
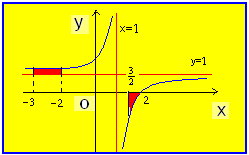
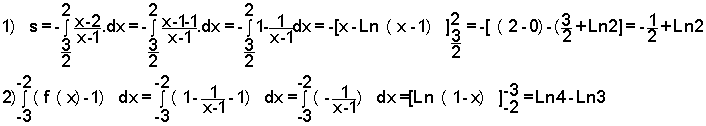
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
20)
احسب مساحة السطح المحصور بين المحور
ox والخط البياني
للتابع f المعرف على R
وفق :
![]()
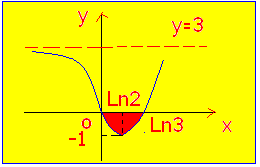
الحل : نرتب التابع ومن ثم نشتق فنجد
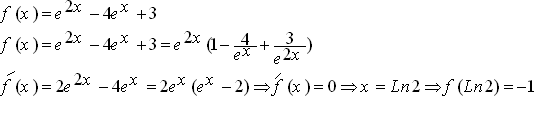
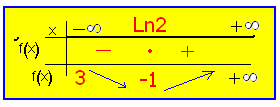
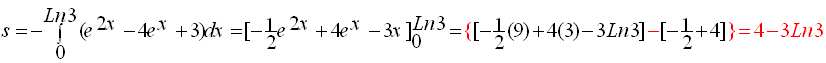
وحدة المساحة
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
21)
احسب مساحة السطح المحصور بين المحور
ox والخط البياني
للتابع f المعرف على
R وفق :
![]()
الحل :
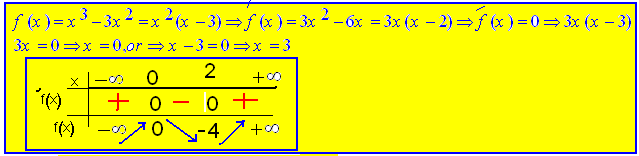
التقاطع مع المحاور
![]()
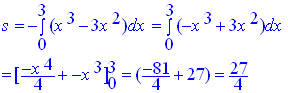
وحدة المساحة
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
22) ليكن ؟
الخط البياني للتابع f المعرف
على R وفق
![]()
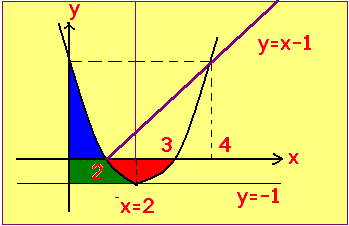
1) ارسم الخط البياني
2) احسب s1 مساحة السطح المحصور بين الحط البياني و ox
3) احسب s2 مساحة السطح المحصور بين الخط البياني والمحورين ox oy
4 ) احسب s3 مساحة السطح المحصور بين الخط البياني والمحورين الإحداثيين والمستقيم الذي معادلته : 1 -=y
5) احسب s4 مساحة السطح المحصور بين الخط البياني والمستقيم 1-x=y
الحل :
![]() نلاحظ
انه يمثل قطع مكافئ مركزه (1-و2) التقاطع مع المحاور :
3=x=1 , x
نلاحظ
انه يمثل قطع مكافئ مركزه (1-و2) التقاطع مع المحاور :
3=x=1 , x
لان
![]()
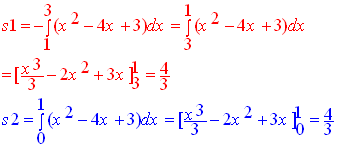
أن 3 s مساحة المستطيل ناقص نصف s2
![]()
تقاطع الخط الباني مع المستقيم
![]() هما
هما
![]()
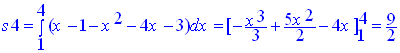
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
22)
ليكن ؟1 الخط البياني للتابع 1f
و المعرف على R وفق
: ![]() وليكن ؟ 2 الخط
البياني للتابع 2f المعرف على
R وفق :
وليكن ؟ 2 الخط
البياني للتابع 2f المعرف على
R وفق :![]()
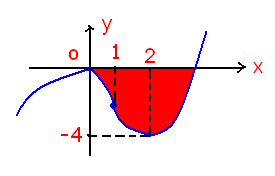
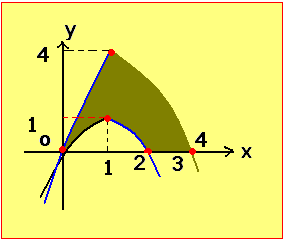
1) ارسم كلا من الخطيين البيانيين السابقين:
2) احسب مساحة السطح المحصور بين 1؟ و 2؟
الحل :
نرسم الجطيين البيانيين ![]()
قطع مكافىء مركزه (2,4) و التقاطع مع المحاور : (0 ,4) و (0 ,0)
![]() نلاحظ انه يمثل قطع مكافئ مركزة (1 ,1) التقاطع
مع المحاور (0 ,2) و(0 ,0)
نلاحظ انه يمثل قطع مكافئ مركزة (1 ,1) التقاطع
مع المحاور (0 ,2) و(0 ,0) ![]() عندما
عندما ![]() الخط البياني ل2 f
تقع فوق الخط البياني 1f
الخط البياني ل2 f
تقع فوق الخط البياني 1f
عندما ![]() الخط البياني ل2 f
تقع تحت الخط البياني 1f
الخط البياني ل2 f
تقع تحت الخط البياني 1f
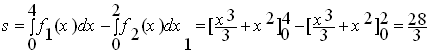
وحدة المساحة
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
24)
ليكن 1؟ الخط البياني للتابع 1f
المعرف على R ,tr :
![]() وليكن
2؟ الخط البياني للتابع 2 f المعرف
على R وفق
وليكن
2؟ الخط البياني للتابع 2 f المعرف
على R وفق
![]()
أحسب مساحة السطح المحصور بين الخطيين البيانيين السابقين
الحل :
![]() قطع مكافئ مركزه
( 4- , 2 )
قطع مكافئ مركزه
( 4- , 2 )
التقاطع مع المحاور الاحداثية
![]()
التابع الثاني :
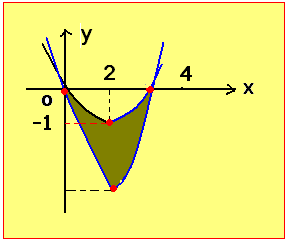
![]() قطع مكافئ مركزه ( 1- , 2
)
قطع مكافئ مركزه ( 1- , 2
)
التقاطع مع المحاور الاحداثية :
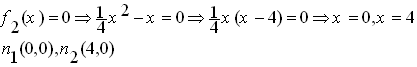
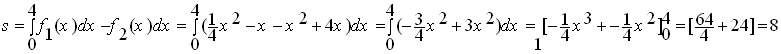
| الصفحة الرئيسية | مقدمة | الأهداف | الرياضيات 1 | الرياضيات2 | رياضيات3 | المنتدى | المصادر | البحث | عداد الزوار | من نحن | اتصل معنا |