الدائرة المثلثية

الصفحة الرئيسية

مقدمة

الأهداف

الرياضيات 1

الرياضيات2

رياضيات3

المنتدى

المصادر

البحث

عداد الزوار

من نحن

اتصل معنا

الدائرة المثلثية : هي دائرة موجه نصف قطرها واحد وذات جهة موجبة إذا كان الدوران بعكس اتجاه عقارب الساعة وعكس عقارب الساعة هي الجهة السالبة

إذا كان لدينا دائرة مركز

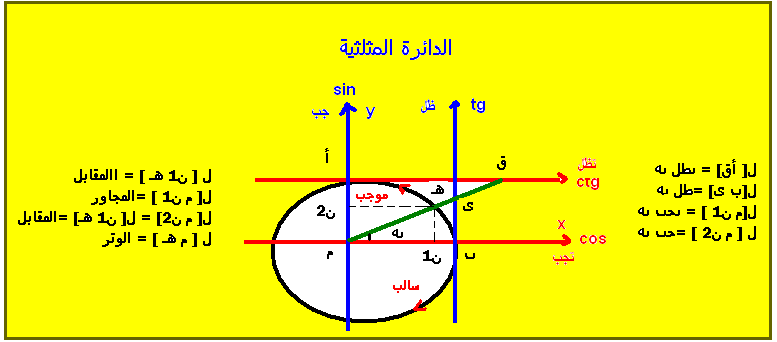
النسب المثلثية لزوايا الشهيرة :

الزاوية	0	15	30	45	60	75	90	105	180	270	360

sin
cos
tg
ctg

الربع الأول من الدائرة المثلثية فيها جميع النسب المثلثية موجبة 0

الربع الثاني = = = = sin الزاوية موجب وباقي النسب المثلثية سالبة

الربع الثالث = = = = tg وctg موجب = = = =

الربع الرابع = = = = cos الزاوية موجب وباقي النسب المثلثية سالبة

مجموعة الدساتير الاساسية :

النسب المثلثية الشهيرة:

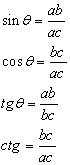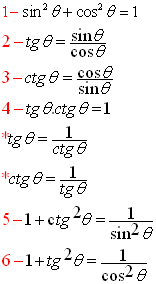الزوايا المتكاملة والزوايا المتتامة :

الزوايا السالبة(المتناظرة)	لزوايا المتكاملة(180 درجة)	اذا كان a-b-c زوايا مثلث	الزوايا المتتامة(90درجة)	اذا كان a-b-c زوايا مثلث

الزوايا (15 -75 - 105 )

105و75 متكاملتان

15 و 75 متتامتان

ملاحظات هامةالإرجاع الى الربع الأول:نقصد بذلك ربط الزوايا الموجودة في الأرباع ( الثاني-الثالث-الرابع)بزوايا موجودة في الربع الأول

إذا كانت زوايا مكتوبة بدلالة أو نعمل مايلي

نحدد الإشارة حسب الربع الذي تقع فيه الزاوية ثم نترك نفس النسبة المثلثية ولكن للزاوية الحادة

إذا كانت زوايا مكتوبة بدلالة أو نعمل مايلي:

نحدد الإشارة حسب الربع الذي تقع فيه الزاوية ثم نبدل النسبة نحذف ت ان كانت موجودة ونضيف إذا كانت غير موجودة لنسبة المثلثية ولكن للزاوية الحادة

دساتير اساسية في المثلثات :

المتطابقات التسب المثلثية

دساتير فرق ومجموع زاويتن

دساتير ضعف الزاوية

مربع النسب المثلثية بدلالة تجب الزاوية

دساتير جداء الى المجموع

دساتير المجموع الى الجداء

المعادلات المثلثية البسيطة:

معادلة الجيب

لها حلان

حالات خاصة

معادلة التجيب حالات خاصة