تناظر الخطوط البيانية للتوابع العددية

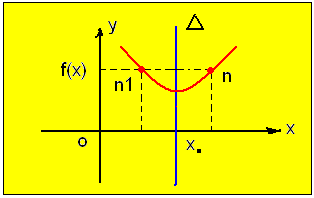
أولاً: التناظر بالنسبة إلى مستقيم ∆ يوازي المحور العينات :

إلى المستقيم ∆ الذي معادلته هو

وإذا تحقق هذا التناظر قلنا إن ∆ هو محور تناظر للخط البياني

 حالة خاصة التناظر بالنسبة إلى المحور العينات:

إذا كان ∆ منطبقاً على المحور العينات فإن معادلة ∆ هي  0 = x  عندئذ الشرط اللازم والكافي ليكون الخط البياني

متناظراً بالنسبة إلى المحور العينات هو

وفي هذه الحالة نقول إن التابع  f تابع زوجي

ملاحظة : إذا كان ؟ الخط البياني للتابع f  المعرف على X  وكان ؟1 نظير ؟ بالنسبة إلى المستقيم ∆ الذي معادلته فإن هو الخط البياني للتابع  f1 المعرف على

  وفق

ثانياً  : التناظر بالنسبة إلى نقطة : إذا كان ؟ الخط البياني للتابع  f  المعرف على X  عندئذ الشرط اللازم و الكافي ليكون  ؟ متناظراً بالنسبة الى النقطة هو

وإذا تحقق هذا التناظر قلنا إن    Oo  هي مركز تناظر الخط البياني ?

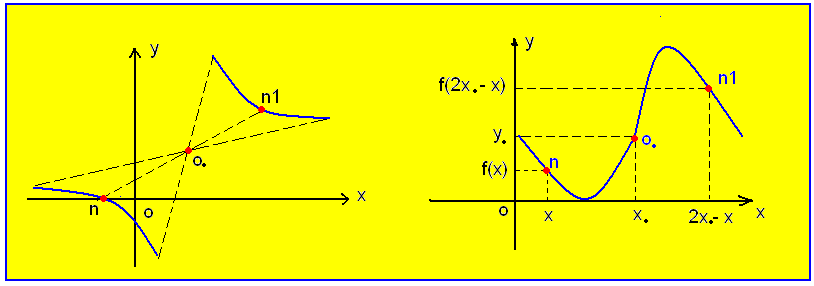
حالة خاصة  : التناظر بالنسبة إلى مبدأ الجملة الديكارتية      (0,0)o : إذا كان ؟ الخط البياني للتابع   f  المعرف على  X  عندئذ الشرط اللازم والكافي ليكون ؟ الخط البياني

متناظراً بالنسبة إلى   (0,0)o    وفي هذه الحالة نقول إن التابع   f  تابع  فردي

ملاحظة : إذا كان ؟ الخط البياني للتابع f  المعرف على X  وكان ؟1 نظير ؟ بالنسبة إلى النقطة فإن ؟1 هو الخط البياني للتابع 1 f المعرف على

وفق